The reading of the (ideal) ammeter, in the circuit shown in . . .

Question : The reading of the (ideal) ammeter, in the circuit shown in figure, equals : 
(i) I when key K₁ is closed but key K₂ is open.
(ii)I/2 when both keys K₁ and K₂ are closed.

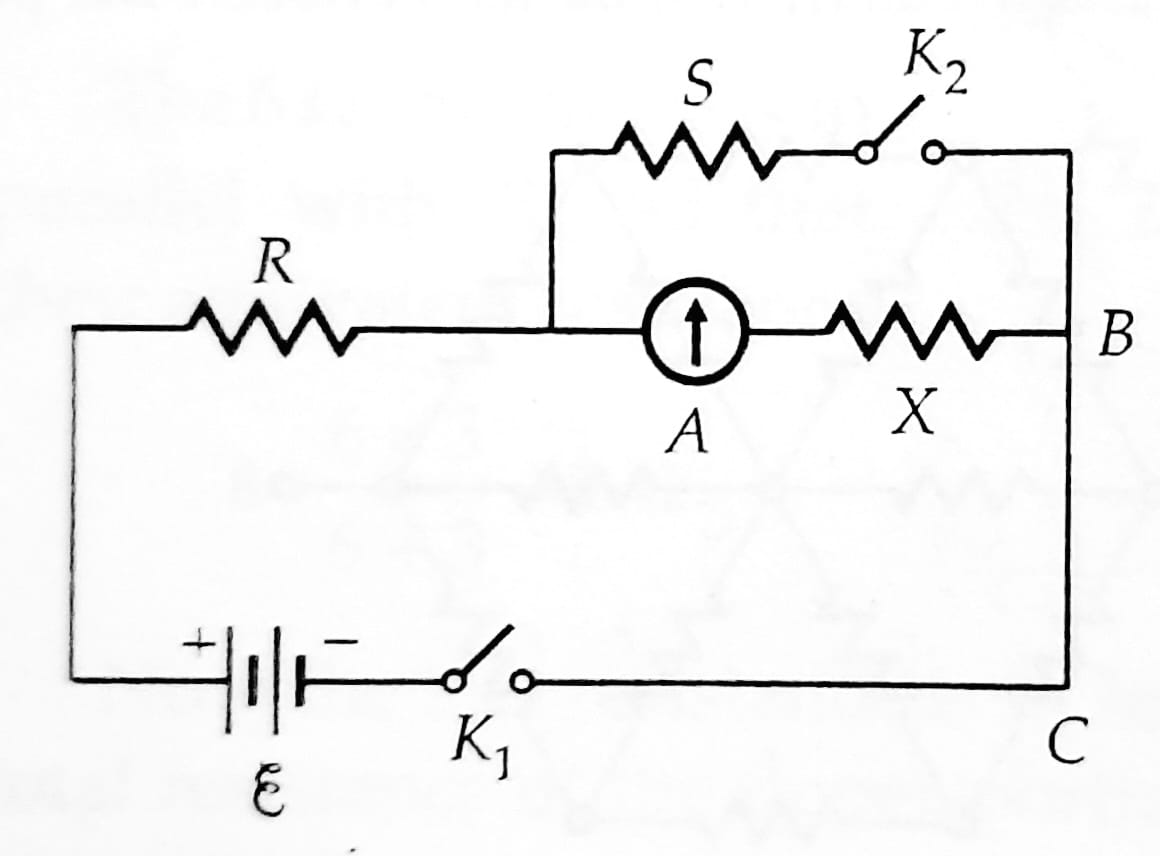
Find the expression for the resistance of X in terms of the resistances of R and S.  

Doubt by Zoya

Solution : 

Here ammeter used is an ideal one this is why we are not including the resistance of Ammeter.

Let us first consider the case (i) When the Key K₁ is closed but key K₂ is open. 

No Current will pass through the the resistance 'S' because the key K₂ is open so the resistance 'S' should not be considered to be the part of the circuit. 

So the total resistance of the circuit will be 
Req=(R+X)
So the current in the ammeter will be given by 
I = ε/Req
I = ε/(R+X) — (1)

Now consider the case (ii) When both the keys K₁ and K₂ are closed. 

Here, the resistance 'S' and 'X' are connected in parallel while the resistance 'R' is connected in series.
So the total resistance in this case will be given as 
R'eq = R+[SX/(S+X)]

Let I' be the current drawn from the battery in this case then 

Clearly the resistance 'S' and 'X' are connected in parallel. So both of them will have the same potential. 

Potential across S = Potential across X

(I'-I/2)S = (I/2)X
I'S-(1/2)S = (I/2)X
I'S = (I/2)X+(I/2)S
I'S = (I/2)(X+S)

Substituting the value of I' and I from equation (1) and (2)

2S(R+X)=R(S+X)+SX
2SR+2SX=RS+RX+SX

2RS-RS=RX+SX-2SX
2RS-RS=RX-SX
RS = X(R-S)
RS/(R-S) = X

Hence, the required value of X in terms of R and S is