Apply Kirchhoff's rules to the loops ACBPA and ACBQA to . . .

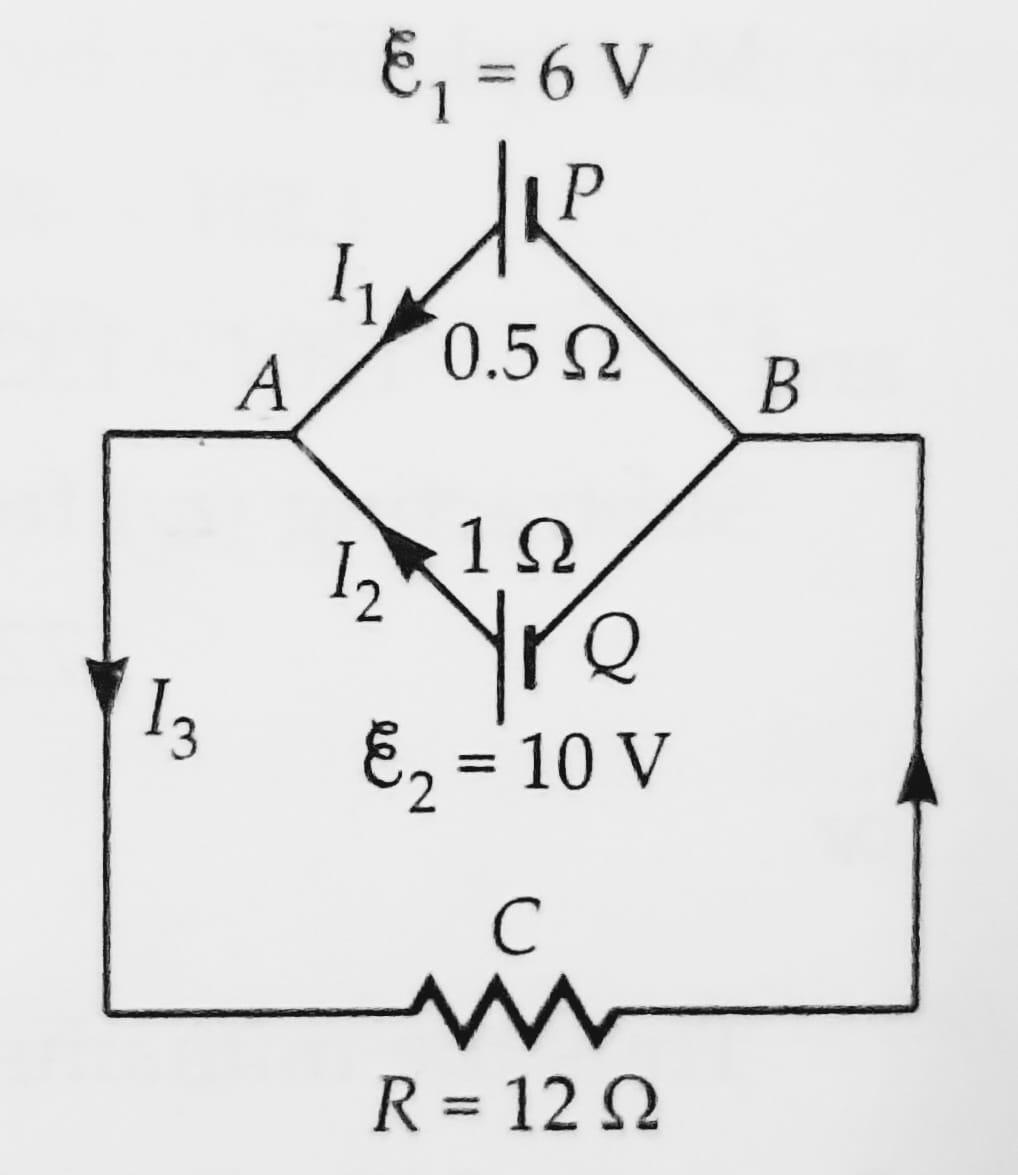
Question : Apply Kirchhoff's rules to the loops ACBPA and ACBQA to write the expression for the currents I₁, I₂ and I₃ in the network shown in figure.

Doubt by Saif

Solution : 

Let the internal resistance of cell of emf ε₁ be r₁ and that of ε₂ be r₂.

ε₁=6V

r₁=0.5Ω

ε₂=10V

r₂= 1Ω

Applying Kirchhoff's Junction Rule at Junction A

I₃=I₁+I₂ — (1)

Applying Kirchhoff's Loop Rule in closed loop ACBPA

12I₃+0.5I₁=6
12(I₁+I₂)+0.5I₁=6 [∵ Using eq (1)]

12I₁+12I₂+0.5I₁=6

12.5I₁+12I₂=6 — (2)

Applying Kirchhoff's Loop Rule in closed loop ACBQA

12I₃+1I₂=10

12(I₁+I₂)+I₂=10 [∵ Using eq (1)]

12I₁+12I₂+I₂=10 
12I₁+13I₂=10 — (3)

Solving equation (2) and (3) by elimination method

[12.5I₁+12I₂=6 ] ×13

[12I₁+13I₂=10] ×12

162.5I₁+156I₂=78

144.0I₁+156I₂=120
_          _            _
________________
18.5I₁  +   0    = -42
----------------------------

I₁ = -42/18.5
I₁ =  -420/185
I₁ = -84/37 A

[-ve sign shows that the actual direction of current I₁ is actually opposite to what is being shown in the figure]

Putting in equation equation (3)

12(-84/37)+13I₂=10 
-1008/37+13I₂=10

13I₂=10+1008/37
13I₂=(370+1008)/37

13I₂=1378/37
I₂ = 1378/(37×13)
I₂ = 106/37 A

Putting the values of I₁ and I₂ in equation (1)

I₃ = -84/37+106/37

I₃ = 22/37 A

Hence, the magnitude of current I₁, I₂ and I₃ is -84/37 A, 106/37 A and 22/37 respectively.